Modulus:
Algoritmi RSA - kuptimi matematik
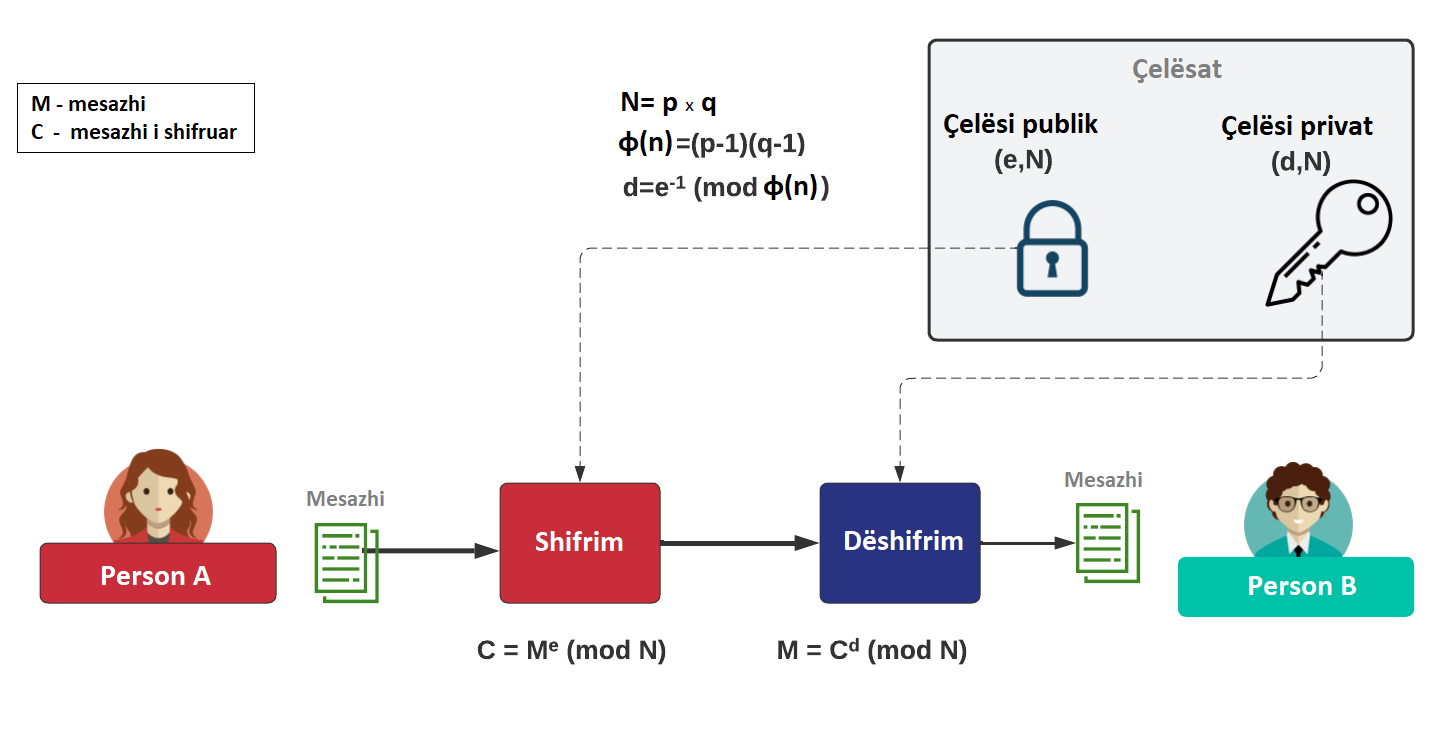
Çelësi publik (public key) dhe ai privat (private key) janë të lidhur matematikisht.
Supozojmë se
PersonA dergon mesazh te shifruar(kriptuar) te
PersonB.
PersonA e shifron mesazhin nëpërmjet çelësit publik të
PersonB.
Ky i fundit ka çelësin e tij privat, ndaj vetëm
PersonB ka mundësi ta dëshifrojë(dekriptojë) mesazhin.
PersonA që është shifruesi, nuk ka mundësi dëshifrimi.
Në procesin e shifrimit ka marrë pjesë vetëm çelësi publik i
PersonB, ndaj vetëm korrelacioni i tij (çelësi privat) mund të dëshifrojë mesazhin.
Matematikisht:
{e,n} është çelësi publik
{d,n} është çelësi privat
Hapi 1:
PersonB zgjedh 2 numra të thjeshtë (prim numbers)
p dhe
q.
p = 2
q = 7
Në implementimin real
p dhe
q janë numra shumë të gjatë.
Me numrat p dhe q në llogarisim modulus
n, ku n = q * q
Pra,
n = p * q = 2 * 7 = 14
Hapi 2:
Hapi i dytë është pak më i komplikuar, këtu ne do të gjejmë sa numra të thjeshtë gjenden midis 0 dhe 14.
Numër i thjeshtë - quhet numri natyror i cili ka vetëm 2 pjesëtues të ndryshëm, vetveten dhe numrin 1.
p.sh. numri 3 është i thjeshtë. Numri 6
nuk është i thjeshtë sepse ai përveçse pjestohet me veten dhe me numrin 1, ka pjestues edhe numrin 2 dhe numrin 3.
Për këtë qëllim do të përdorim teoremen e Tejlorit:
φ(n)=(p-1)(q-1)=(2-1)(7-1)=1 * 6 = 6
Pra, janë 6 numra të thjeshtë midis 0 dhe 14, që jane: 1,3,5,7,11,13
Hapi 3:
Zgjedhim numrin e plotë
'e' (public exponent
e) nga këta 6 numra.
Numri
'e' duhet të plotësojë 2 kushte:
Kushti i parë: 1 < e < φ(n)
Pra: 1 < e < 6
Kushti i dytë: gcd(e,φ(n))=1
Pra, të jenë bashkë-prime (bashkë-thjeshtë) me φ(n), pra i bashkë-thjeshtë me 6.
Nga kushti i parë filtrohen vetëm numrat 3 dhe 5.
Nga kushti i dytë përfitojmë numrin
5, sepse numri 5 është ai numër i thjeshtë që është më afër φ(n)=6
Hapi 4:
Ne përfituam çelësin publik (Publik Key), i cili përmban eksponentin publik
'e' dhe modulus
'n': {e,n} =
{5,14}
Ky është çelësi publik {5,14} që PersonB i jep PersonA dhe kujtdo tjetër që do të shifrojë mesazhe për atë. PersonA do ta përdori këtë çelës publik për çdo mesazh të kriptuar që do t'i dërgojë PersonB.
Për të gjeneruar çelësin privat të PersonB, na duhet
{d,n} . Deri tani kemi n = 14.
Le të llogarisim vlerën e
'd'
Formula është
e * d = 1 mod φ(n)
Pra, d * 5 mod 6 = 1
Mund të kemi
d=5 ( sepse 5 * 5 = 25 mod 6 = 4 mbetja 1 )
Mund të kemi
d=11 ( sepsse 11 * 5= 55 mod 6 = 9 mbetja 1 )
Mund të kemi
d=17 ( sepsse 17 * 5= 85 mod 6 = 14 mbetja 1 )
etj,
Shembull:
10000 mod 23 = X
10000 / 23 = 434,782
Pra, numri 23 hyn 434 herë te numri 10000
23 * 434 = 9982
Kështu që 10000 - 9982 = 18
X = 18
Në mënyrë rastësore ne zgjedhim njërin prej tyre, në këtë rast po zgjedhim
d = 11
Kështu formojmë çelësin privat {d,n} =
{11,14}
Këtë çelës privat PersonB do ta mbajë për vete sepse do të shërbejë për dekriptim.
Hapi 5
Supozojmë se PersonA do të dërgojë mesazhin
'k' te PersonB.
çelësi publik i PersonB ështe {e,n} =
{5,14}
k < n
Po ta kthejmë
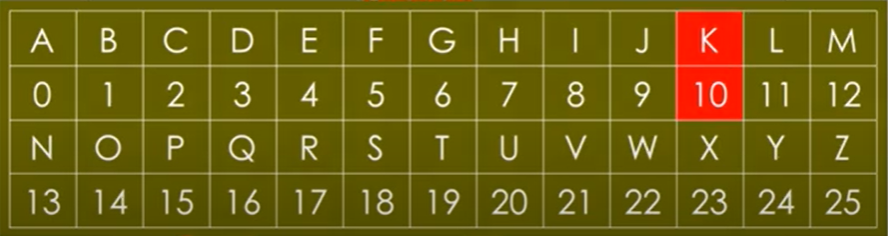
k në vlerë numerike, ajo është k=10 ( sepse a=0, b=1,c=2 .... z=25 )
Pra 10 < 14
Atëherë lë të përdorim këtë formulë për të marrë një tekst të koduar:
c = (vlera k)
e mod n
Pra, c = 10
5 mod 14 = 12
Pra teksti i koduar (ciphertext) është
12
Pra PersonA po i dërgon PersonB numrin 12 në kanalet publike, kushdo që e lexon shifrën 12 nuk e njeh dot kuptimin e saj.
Hapi 6:
Dekriptimi nga PersonB.
PersonB do të përdori çelësin e tij privat për ta dëshifruar kodin
12
çelësi privat është {d,n} =
{11,14}
dekriptimi = (kodi shifruar)
d mod n
Pra
, dekriptimi = 12
11 mod 14 = 10
Pastaj përdor tabelën (e mësipërme) për të parë cilës shkronjë i perket numri
10, ku dallohet që ajo i përket shkronjës
'k'
Në kod (.NET 4.7.2):
using System.Security.Cryptography;
Personi që ka
'rs1' do të shifrojë mesazhin sekret me çelësin publik të
'rs2'. Vetëm
'rs2' do të ketë mundësinë të dëshifrojë mesazhin duke përdorur çelësin e tij privat.
RSA rs1 = new RSACng();
RSA rs2 = new RSACng();
Sipas dëshirës mund të përdorim klasën
RSA ose
RSACng (RSA Cryptography Next Generation).
string pubkey2 = rs2.ToXmlString(false);
string privkey2 = rs2.ToXmlString(true);
Lexojmë parametrat e rs2:
RSAParameters param = rs1.ExportParameters(true);
// në konstruktor vendoset 'true' për të lexuar të dhënat e çelësit privat. Për të lexuar vetëm të dhënat e çelësit publik vendos
false
" P => "+ Convert.ToBase64String(param.P).ToString()
" Q => " + Convert.ToBase64String(param.Q).ToString()
"Public exponent E => " + Convert.ToBase64String(param.Exponent).ToString()
"Private exponent D => " + Convert.ToBase64String(param.D).ToString()
"Modulus N = P * Q => " + Convert.ToBase64String(param.Modulus).ToString()
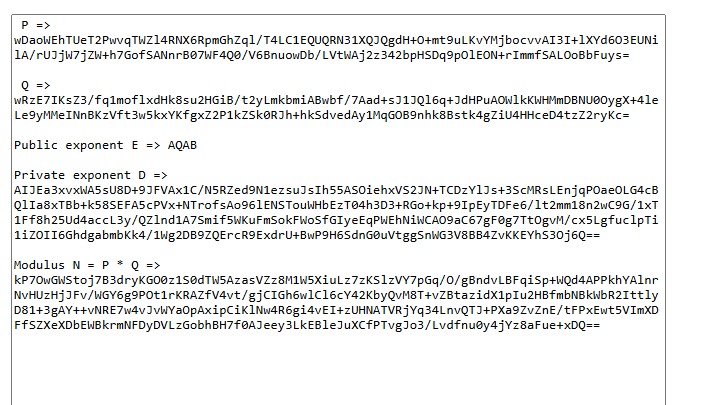
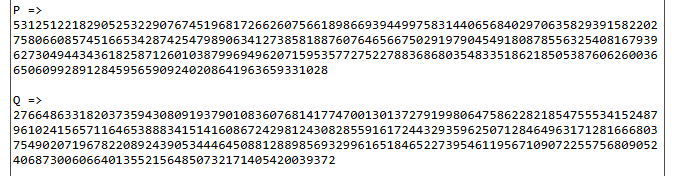
Nga rezultati i mësipërm shih me kujdes
P dhe
Q

Këtu
P dhe
Q nuk janë numra.
Për t'i konvertuar në numra
integer do të përdorim klasën
System.Numerics
RSAParameters param = rs2.ExportParameters(true);
BigInteger bQ = new BigInteger(param.Q);
string qVlera = "Q => " + bQ.ToString()
Para se të shifrojë mesazhin sekret,
'rs1' duhet të importojë çelësin publik të
'rs2':
rs1.FromXmlString(pubkey2);
Mesazhi sekret konvertohet ne varg bajtesh (byte[]):
var msgBajte = UTF8Encoding.UTF8.GetBytes("Ky është mesazh sekret!");
Për enkriptim do të veprojë
'rs1'
var bajteEnkriptuar = rs1.Encrypt(msgBajte, RSAEncryptionPadding.OaepSHA512);
Për dekriptim do të veprojë
'rs2'
var bajteDekriptuar = rs2.Decrypt(bajteEnkriptuar, RSAEncryptionPadding.OaepSHA512);
Në fund, konvertojmë byte[] në tekst.
string tekstiPaster = System.Text.Encoding.UTF8.GetString(bajteDekriptuar).ToString();
tekstiPaster = "Ky është mesazh sekret!";
Përfundime:
Algoritmi
RSA shifron me çelës (publik) me gjatësi maksimale 2048 bit.
Kjo tregon se shifrimi është shumë i fortë.
Por RSA mund të shifrojë (enkriptojë) vetëm blloqe të dhënash që janë më të shkurtra se gjatësia e çelësit.
Pra, nuk mund të shifrojë
skedarët
Për të shifruar (enkriptuar) skedarët
unë ndjek praktikën e kombinimit me algoritmin simetrik
AES, sipas hapave të mëposhtëm.
Shifrimi
-
gjenerohet çelësi simetrik dhe IV (Initialization Vector) për enkriptimin simetrik me AES
-
shifrohet (enkriptohet) skedari me AES (simetrik) duke përdorur çelësin dhe IV të përmendura më sipër.
-
Çelësi dhe IV së bashku me të dhëna plotësuese, vendosen në një strukturë të dhënash e cila më pas shifrohet me çelësin publik RSA.
-
struktura e shifruar me RSA injektohet në skedarin e shifruar me AES.
Dëshifrimi
-
nxirret struktura e të dhënave që u injektua në skedarin e shifruar.
-
dëshifrohet struktura e të dhënave nëpërmjet çelësit privat RSA.
-
nga struktura veçohet çelësi AES, kodi IV dhe të dhënat plotësuese.
-
dëshifrohet skedari duke përdorur algoritmin AES (çelësin simetrik + IV )
-
gjenerohet skedari i pastër.
Ju mund të testoni versionin desktop
"PotEncrypt.exe", ose versionin
online duke përdorur shërbimin
RSA file service