Kurbat Eliptike ECC (Elliptic Curve Cryptography)
Hyrje
Në kriptografinë me çelësa publik e privat, qëllimi është të shkohet nga A => B, por jo B => A në të njëjtën formë.
Po të krahasojmë
ECC me
RSA, për të njëjtin shifrim ku ECC kërkon një gjatësi çelësi
256 bit, algoritmi RSA kërkon
3072 bit.
Nëse gjatësinë e çelësit ECC e rrisim në
384 bit, për RSA do të duhen
7680 bit për të mbajtur të njëjtin nivel sigurie.
Pra, madhësia e çelësit të ECC është më e vogël se ajo e RSA për të njëjtin nivel sigurie.
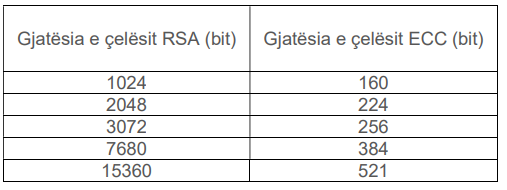
Nuk ka një marrëdhënie lineare midis madhësive të çelësave ECC dhe çelësave RSA. Kjo do të thotë, një madhësi çelësi RSA që është dy herë më e madhe nuk përkthehet në një madhësi çelësi ECC që është dyfishuar.
Ky ndryshim tregon se gjenerimi dhe nënshkrimi i çelësave ECC është dukshëm më i shpejtë se për ato RSA, dhe gjithashtu ECC përdor më pak memorie sesa RSA.
Edhe shpejtësia e shifrimit dhe e dëshifrimit është mesatarisht më e lartë në
ECC.
Disavantazhi kryesor i ECC qëndron në faktin se nuk është i lehtë për t'u zbatuar në mënyrë të sigurt. Krahasuar me RSA-në, e cila është më e thjeshtë si në aspektin e verifikimit ashtu edhe në atë të enkriptimit,
Në dallim nga
RSA,
ECC e bazon qasjen e saj ndaj sistemeve kriptografike me çelës publik në mënyrën se si
kurbat eliptike strukturohen në mënyrë algjebrike mbi
fusha të fundme. Prandaj, ECC krijon çelësa që janë më të vështirë, matematikisht, për t'u deshifruar.
Për këtë arsye, ECC konsiderohet të jetë implementimi i gjeneratës së ardhshme të kriptografisë me çelës publik dhe më i sigurt se RSA.
Për shkak të gjatësisë më të shkurtër të çelësit se RSA, bën sens të pohojmë se
ECC mud të përdoret edhe për të ruajtur nivele të larta të
performancës përveç asaj të
sigurisë.
RSA është shumë e fortë, ajo mbështetet në faktin se shumëzimi i numrave të thjeshtë për të marrë një numër më të madh është i lehtë, ndërsa faktorizimi i numrave të mëdhenj përsëri në numrat e thjeshtë origjinalë është shumë më i vështirë.
Megjithatë, për të mbetur i sigurt, algoritmi
RSA ka nevojë për çelësa që janë
2048 bit ose më të gjatë.
Por kjo e bën procesin të ngadaltë. Pra, madhësia e çelësit është e rëndësishme.
Ekzistojnë disa
dobësi të mundshme ndaj kriptografisë me kurbë eliptike, duke përfshirë
- sulmet anësore të kanalit
- sulmet e sigurisë me përdredhje
Të dy llojet synojnë që të bëjnë të pavlefshëm sigurinë e ECC-së për
çelësat privatë.
Një rrezik tjetër për
ECC vjen nga kompjuterat kuantik. Një konfuzion ka lindur nga komentet e
NSA-së për aftësinë e kompjuterëve kuantikë për të thyer ECC-në.
Për shkak të mungesës së popullaritetit të kompjuterave kunatik, unë mendoj se kjo është ca e parakohshme.
Megjithatë kam bindjen se
siguria, është dhe do të mbetet gjithnjë një proces i vazhdueshëm. Nuk do të ketë kurrë një mjet që do të ofrojë siguri përgjithmonë.
 Kompjuterët kuantikë përdorin kubite ashtu si kompjuterët normalë
që përdorin tranzistorë.
Kompjuterët kuantikë përdorin kubite ashtu si kompjuterët normalë
që përdorin tranzistorë.
Ndryshe nga tranzistorët që janë ose të ndezur
ose të fikur, kubitet janë mbivendosje të të ndezurit dhe të fikurit.
Duhen disa kubite për të krijuar një portë, ashtu siç duhen disa tranzistorë
për të krijuar një portë NAND.
Gjatë pesë viteve të fundit, numri i kubiteve në një njësi sipërfaqeje është
dyfishuar nga viti në vit.
Në vitin 2017 u publikua një punim mbi mënyrën e thyerjes së ECC duke
përdorur kompjuterë kuantikë.
Autorët tregojnë se si të krijohen porta (gates) që do të zgjidhin problemin
e logaritmit diskret në kurbat eliptike për të gjetur çelësin.
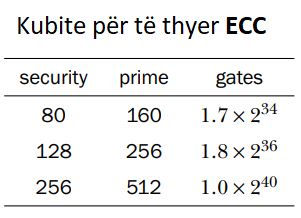
Sot, ka 1.7 × 28 kubit në pajisjen më të madhe të raportuar. Kjo është
rreth 26 porta.
Kjo do të thotë se do të duhen të paktën 30 vjet para se ECC të thyhet nga
kompjuterët kuantikë, duke supozuar se koha e dyfishimit prej një viti
mund të mbahet për të gjithë këtë kohë.
ECC përdor algoritme të bazuara në vetitë e kurbave eliptike për të gjeneruar çelësa. Gjenerimi i çelësave përfshin zgjedhjen e një çelësi privat dhe më pas nxjerrjen e një çelësi publik përkatës duke përdorur vetitë e kurbës eliptike.
Algoritmet kryesore të përfshira në gjenerimin e çelësave ECC janë:
- ECDSA(Elliptic Curve Digital Signature Algorithm) => Ky algoritëm përdoret për krijimin dhe verifikimin e nënshkrimeve dixhitale, duke siguruar vërtetësinë dhe integritetin e të dhënave.
Ky algoritëm gjeneron çelësa
- ECDH(Elliptic Curve Diffie-Hellman) => Ky algoritëm lehtëson krijimin e një çelësi sekret të përbashkët midis dy palëve përmes një kanali të pasigurt.
Ky algoritëm gjeneron çelësa
- ECIES(Elliptic Curve Integrated Encryption Scheme) =>Kjo skemë kombinon çelësin dhe enkriptimin në një proces të vetëm.
- EdDSA(Edwards-curve Digital Signature Algorithm) => Ky është një tjetër algoritëm nënshkrimi që përdor kurba të përdredhura të Edwardsit, duke ofruar një qasje të ndryshme ndaj gjenerimit të nënshkrimeve.
- MQV (Menezes–Qu–Vanstone ) është një protokoll i pranuar për marrëveshjen e çelësave bazuar në skemën Diffie–Hellman . Ashtu si skemat e tjera të Diffie–Hellman, MQV ofron mbrojtje kundër një sulmuesi aktiv. Protokolli mund të modifikohet për të funksionuar në grupet e kurbave eliptike, ku njihet si kurba eliptike MQV (ECMQV).
Algoritmi ECMQV gjeneron çelësa
Kuptimi matematik
Të kuptuarit matematikor të
ECC është ende sfidues, veçanërisht për ata që nuk kanë një doktoraturë në matematikë.
Studimi im synon mbështetjen e kuptimit bazë matematikor për nevojat e zhvillimit të algoritmeve në gjuhët e nivelit të lartë - konkretisht në .Net.
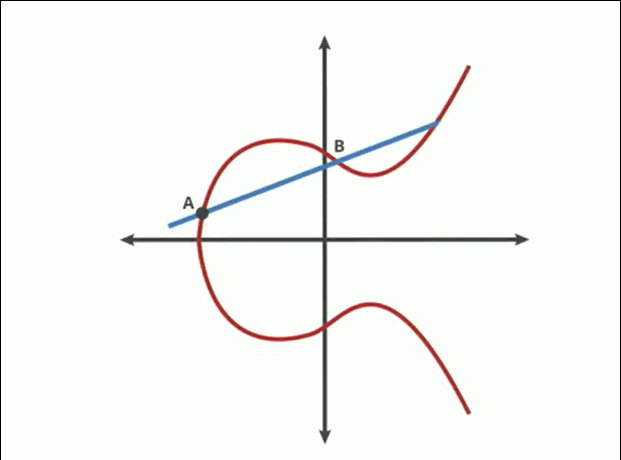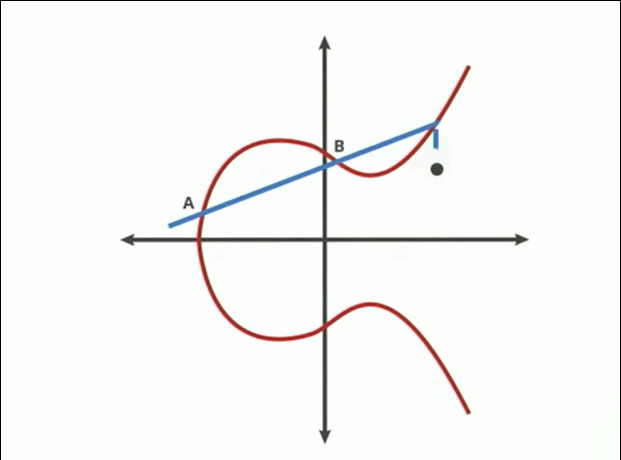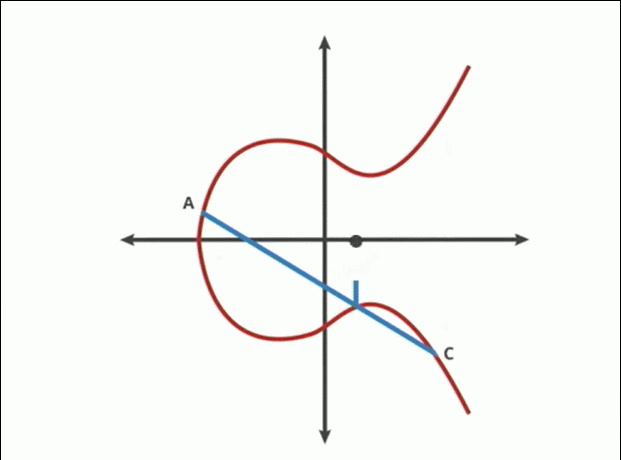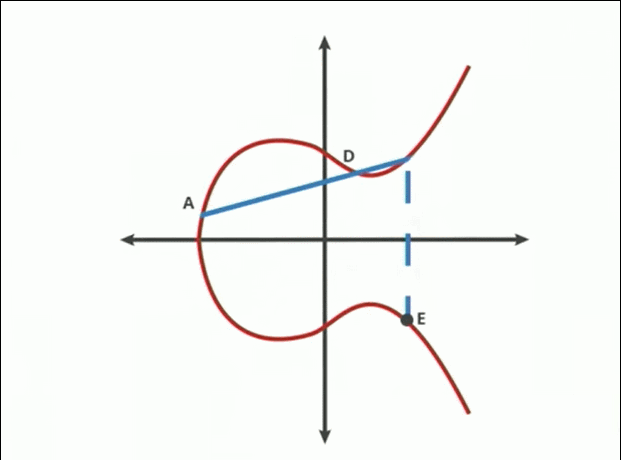
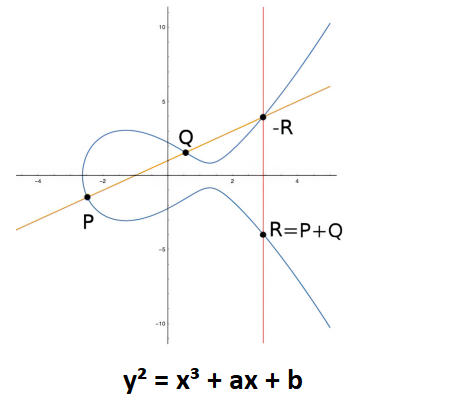
Një kurbë eliptike është një kurbë planare mbi një fushë të fundme e cila përbëhet nga pikat që plotësojnë ekuacionin:
y2 = x3 + ax + b.
Këtu variablat
x dhe
y janë koordinatat, ndërsa
a dhe
b janë koeficientët që përcaktojnë veçantinë e kurbës.
Bazuar në këto koeficientë kurba merr forma të ndryshme.
Shembull:
Për kurbën E : Y2 = X3 - 5X + 8
mund të themi që aty gjendjet pika P=(1,2)
Në këtë shembull të kriptografisë së kurbës eliptike, çdo pikë në kurbë mund të pasqyrohet mbi boshtin
X dhe kurba do të mbetet e njëjtë.
Çdo vijë jo-vertikale do ta presë kurbën në
tre vende ose më pak (
sepse mund të ndodhi që nga gjenerimi rastësor P dhe Q të jenë në të njëjtin vend, pra do të përftohen vetëm 2 pika. Në këtë rast do heqim tangenten horizontale mbi këtë pikën e njëjtë P dhe Q).
Shuma e dy pikave në një kurbë eliptike është pika negative e pikës së kryqëzimit me kurbën e një vije të vizatuar midis tyre.
Shkëmbimi i çelësave sipas Diffie-Hellman
Për një grup
G marrim një element
g nga ai grup ( g ∈ G ).
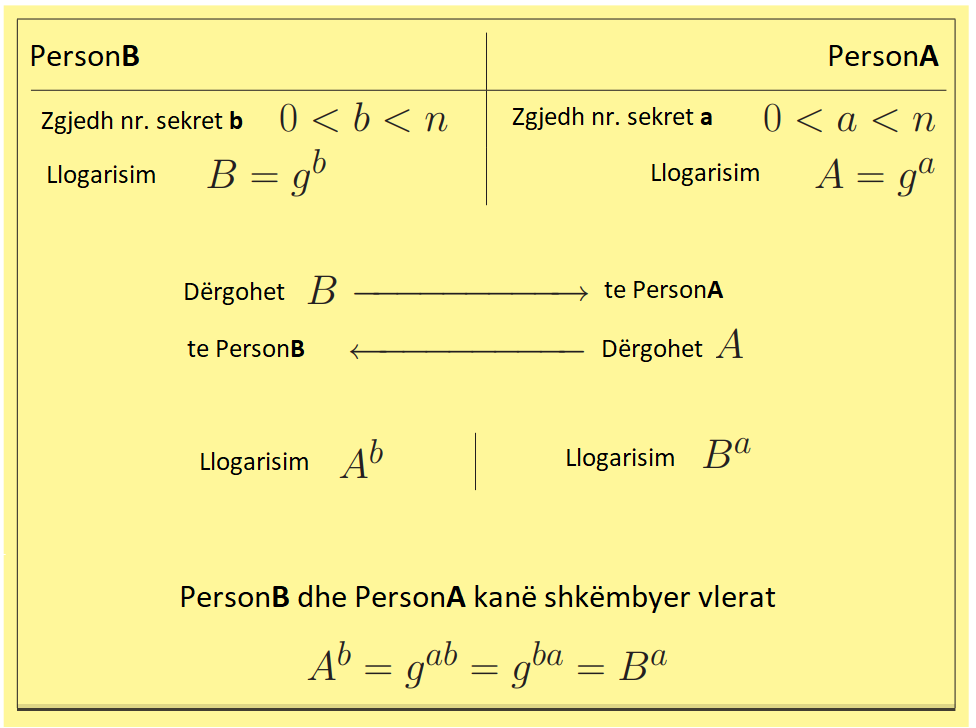
Avantazhi i shkëmbimit të çelësave të kurbës eliptike është se çelësat nuk kanë nevojë të ruhen; ato mund të llogariten sa herë që nevojiten.
Në shkëmbimin e çelësave të kurbës eliptike, të dyja palët llogaritin të njëjtën pikë dhe përdorin vlerën
x për sekretin e përbashkët.
Diffie-Hellman përdor çelësin privat të një personi dhe çelësin publik të një personi tjetër për të krijuar një çelës sekret të përbashkët. Çelësi sekret përdoret me një algoritëm standard të kodimit me një çelës të vetëm.
Algoritmi
MQV kombinon dy çelësa privatë dhe dy çelësa publikë që shumëzohen për të formuar një pikë sekrete të përbashkët. Vlera
x përdoret më pas si çelësi sekret i përbashkët.
Kurbat eliptike të zakonshme mbi fushat e fundme përcaktohen nga ekuacioni
E : y2 = x3 + a4x + a6 mod p
Gjetja e çelësit privat nga
çelësi publik dhe
pika bazë quhet
problemi i logaritmit diskret të kurbës eliptike.
Për kurbat mbi një fushë primi, vështirësia vjen nga madhësia e primit dhe shkon sa rrënja katrore e rendit të pikës bazë.
Pra, një çelës simetrik ekuivalent është gjysma e madhësisë së një çelësi kurbe eliptike.
Mbaj parasysh që kurba eliptike është ende një nivel sigurie eksponenciale.
Në kod (.Net 4.7.2 + Bouncy Castle)
 Shkarko librarinë - 2.55 MB
Shkarko librarinë - 2.55 MB
Libraria e
BC (Bouncy Castle) gjeneron çelësa për algoritmet kryesore
- ECDSA
- ECDH
- ECDHC
- ECGOST3410
- ECMQV
using Org.BouncyCastle.Crypto;
using Org.BouncyCastle.Crypto.Parameters;
using Org.BouncyCastle.Security;
Le të gjenerojmë çelësat
publik dhe
privat për kurbën eliptike
secp256 duke përdorur algoritmin
ECDH (Elliptic Curve Diffie-Hellman).
Kuptimi i secp256
sec (standards for efficient cryptography)
p (kurba eliptike mbi një fushë primi)
256 (gjatesia në bit e fushës së primit)
//krijohet instanca për gjenerim sipas algoritmit të zgjedhur
var gen = new CEBA.Org.BouncyCastle.Crypto.Generators.ECKeyPairGenerator();
//Krijohet variabël i rastësishëm
var secureRandom = new SecureRandom();
//Krijimi i parametrave duke përdorur variablin + gjatësinë e primit (256)
var keyGenParam = new KeyGenerationParameters(secureRandom, keySize);
//Inicializohet për gjenerim algoritmi ECDH me sipas parametrave të mësipërm
gen.Init(keyGenParam);
//Gjenerohet çiftimi i çelësave
return gen.GenerateKeyPair();
Rezultati i përftuar vendoset në variablin
gjCelesa, dhe fillojmë procesin e veçimit të të dhënave.
string cPrivat = gjCelesa.Private;
//leximi i parametrave të çelësit privat
ECPrivateKeyParameters privateKeyParam = (ECPrivateKeyParameters)cPrivat.Private;
//eksponenti privat i deshifrimit brenda çelësit privat
string D = privateKeyParam.D.ToString();
StringWriter tW = new StringWriter();
var pW = new Org.BouncyCastle.OpenSsl.PemWriter(textWriter);
pW.WriteObject(gjCelesa.Public);
pW.Writer.Flush();
string cPublik = tW.ToString();
ECPublicKeyParameters publicKeyParam = (ECPublicKeyParameters)gjCelesa.Public;
string X = publicKeyParam.Q.X.ToBigInteger().ToString();
string Y = publicKeyParam.Q.Y.ToBigInteger().ToString();
Më poshtë çelësi publik:
MDYwEAYHKoZIzj0CAQYFK4EEABwDIgAEqEkOWSUsGeBn0BSPeHaPjVVJkXn
YTlj1k5UA591Wj5c=
Më poshtë çelësi privat:
SXJkaSBCdXphbGkgRUNDIHNlcnZpY2UgTWFqIDIwMjU=
Krahasimi
ECC me çelësat e
RSA për të njëjtin nivel sigurie.

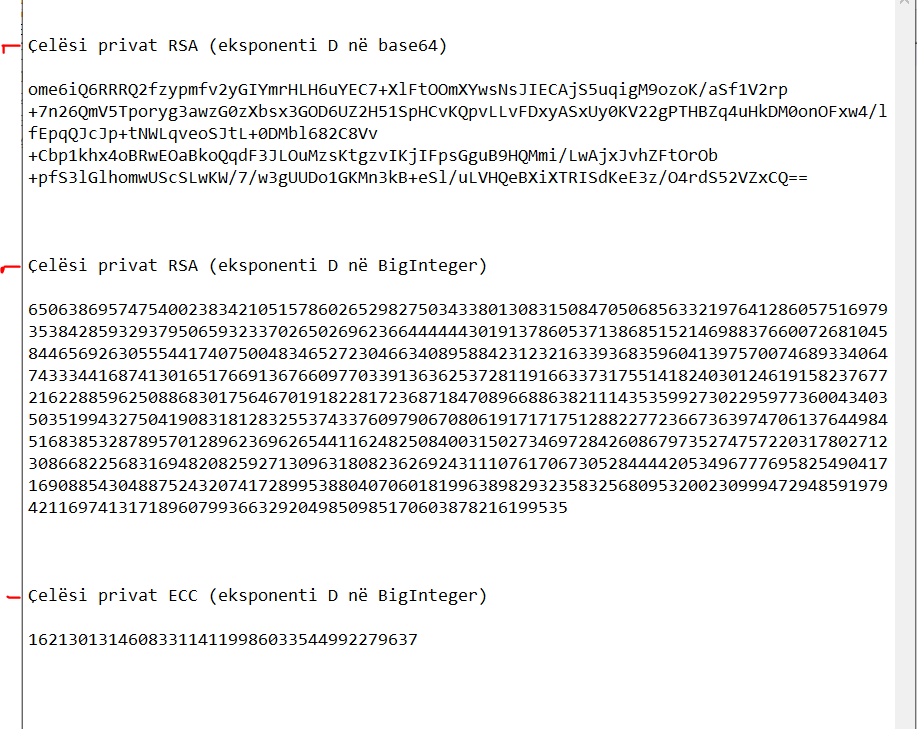
Përfundime
Për të punuar me ECC ndiqen këto hapa.
Shifrimi:
- Përcaktohet kurba eliptike.
- Gjenerohet çifti i çelësave publik e privat duke përdorur atë kurbë, si për dërguesin ashtu edhe për marrësin.
- Gjenerohet një çelës sekret i përbashkët nga çifti i çelësave.
- Nga ai çelës sekret i përbashkët, gjenerohet një çelës enkriptimi.
- Duke përdorur atë çelës enkriptimi dhe algoritmin e enkriptimit simetrik, enkriptohen të dhënat që do të dërgohen te marrësi.
Dëshifrimi
- Dërguesi ose do ta ndajë kurbën me marrësin ose dërguesi dhe marrësi do të kenë të njëjtin përdorim për të njëjtin lloj kurbe.
- Gjithashtu, dërguesi do ta ndajë çelësin e tij publik me marrësin.
- Gjenerohet çifti i çelësave publik privat duke përdorur të njëjtën kurbë për atë kurbë.
- Rigjenerohet një çelës sekret të përbashkët duke përdorur çelësin privat të marrësit dhe çelësin publik të dërguesit.
- Nga ai çelës sekret i përbashkët, gjenerohet një çelës enkriptimi.
- Duke përdorur atë çelës enkriptimi dhe algoritmin e enkriptimit simetrik, dekripto të dhënat.